I. La transformée de Fourier▲
Joseph Fourier (1768-1830) est un mathématicien français qui a démontré que tout signal continu pouvait se décomposer sous la forme de la somme de sinusoïdes. Cette décomposition est réversible et possède d'autres propriétés – conservation de l'énergie, linéarité de l'opérateur…
I-A. La transformée de Fourier continue▲
La transformée de continue s'applique aux fonctions de carré intégrable et les représente par une intégrale pondérée d'exponentielles complexes. La formule est la suivante :
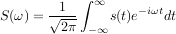
Dans toutes les formules, la fonction en minuscules indique le signal temporel, la fonction en majuscules le signal spectral (en fréquence).
Pour repasser dans l'espace temporel, la formule ne varie pas trop :
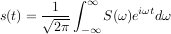
I-B. Les séries de Fourier▲
Découvertes avant leur version plus générale, les séries de Fourier permettent de décomposer une fonction périodique en somme pondérée infinie d'exponentielles complexes de même période. La formule est la suivante, avec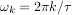 
où 
est la période du signal :
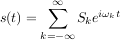
I-C. La transformée de Fourier discrète▲
Si maintenant on discrétise la fonction périodique, on obtient une somme finie d'exponentielles complexes. Cette somme d'exponentielles est elle-même périodique.
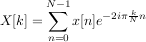
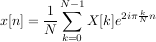
On peut remarquer la différence de notation entre la version continue et la version discrète. Elle est standard, les parenthèses sont associées à un signal continu, les crochets à un signal discret.
On constate aussi un facteur d'échelle présent dans la transformée inverse, mais pas dans la directe. En fait, ce facteur est l'équivalent de celui de la version continue, et on pourrait inverser l'application de ce facteur. En revanche, à cause de lui, le théorème de Parseval – non, non, pas Perceval – n'est plus respecté.
II. Utilisation d'une transformée de Fourier dans la réalité▲
En maths-info, seule la transformée de Fourier discrète est utilisée. En effet, tous les signaux utilisés sont échantillonnés et quantifiés. L'échantillonnage signifie qu'on discrétise l'échelle temporelle ou spatiale – dans le cas d'une image, on travaille sur deux dimensions spatiales, dans le cas d'un signal sonore ou financier, on utilise une dimension temporelle –, la quantification correspond à la discrétisation des valeurs possibles du signal.
II-A. Applications de la transformée de Fourier discrète▲
II-A-1. Analyse du contenu spectral▲
La transformée de Fourier discrète permet d'obtenir un échantillonnage du spectre du signal à transformer. Dans le cas d'un signal multidimensionnel comme une image, on effectuera une transformée de Fourier sur chacune des dimensions. On observera aussi dans ce cas qu'une transformée de Fourier sur une image constituée de lignes sera formée de colonnes, et inversement.
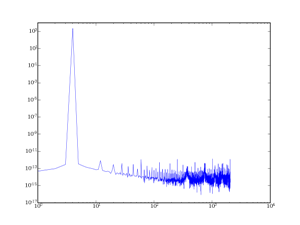
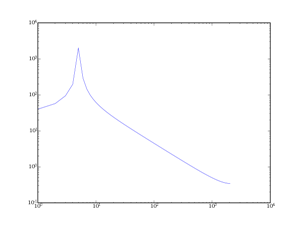
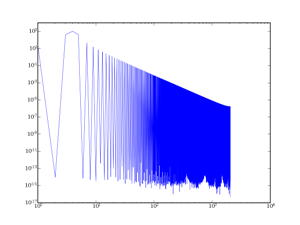
Dans le cas d'une image, on analyse un signal fini dans l'espace. On considère en réalité une image infinie constituée de la même image multipliée à l'infini, d'après la définition de la transformée de Fourier. En revanche, dans le cas d'un signal sonore par exemple, on analysera des morceaux de signal à chaque fois – naturellement, on peut aussi faire la même chose avec une image, mais c'est moins rentable. Le signal n'est donc plus identique à chaque fois, c'est ce qui cause le « leakage » d'une fréquence dans tout le spectre (voir la FFT d'un sinus pur et d'un sinus tronqué au paragraphe II-B-1).
Ces artefacts impliquent l'utilisation de fonctions de fenêtrage. Chacune de ces fonctions modifie le spectre des fréquences, mais elles permettent d'observer des fonctions non périodiques ou apériodiques en minimisant les problèmes de ruptures aux extrémités de la portion de signal analysée.
II-A-2. L'application courante, la convolution▲
Une convolution dans le domaine réel correspond à une multiplication dans le domaine spectral. De plus, une convolution brute a une complexité en O(n²) alors qu'une convolution par transformée de Fourier peut avoir une complexité en O(n log(n) ) en utilisant la FFT, si n est la dimension du signal.
Pour effectuer une convolution dans le domaine spectral, on doit avoir deux spectres de même dimension. De plus, si un signal de taille n est convolué avec un filtre de taille m, le signal résultant est de taille n + m - 1. Dans ce cas, si on prend comme taille de la FFT le maximum de n et m, on obtiendra un signal final périodique de même taille, donc plus petit que la taille du signal résultant par une convolution brute. On est alors en présence d'un repliement de spectre, car les échantillons « disparus » sont en fait additionnés aux autres. On augmente alors la taille du signal et celui du filtre en ajoutant des 0 à la fin pour atteindre la taille critique des n + m - 1.
II-B. Les fonctions de fenêtrage▲
Une fonction de fenêtrage est une fonction par laquelle le signal à analyser est multiplié avant la transformée de Fourier. Cela revient donc à faire une convolution entre les deux spectres dans l'espace des fréquences. Lors de l'analyse d'une tranche de signal, la transformée de Fourier considère que cette tranche se duplique à l'infini, donc si la tranche n'est pas exactement synchronisée avec le signal (ce qui n'arrive en fait jamais, par exemple un signal à 5 Hz vu à travers une fenêtre de 0.5 sec), le signal dont on calcule la transformée de Fourier n'est pas celui qui est analysé en réalité… C'est là l'intérêt des fenêtres, qui permettent de rendre continu le signal analysé, en limitant les effets des fonctions de fenêtrage.
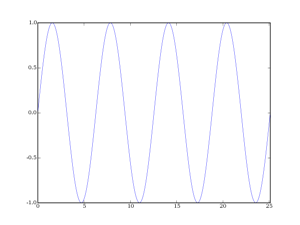
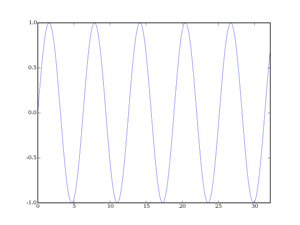
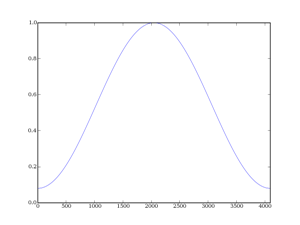
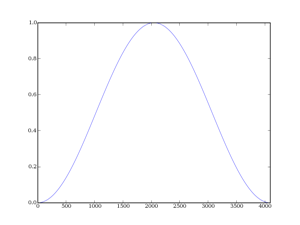
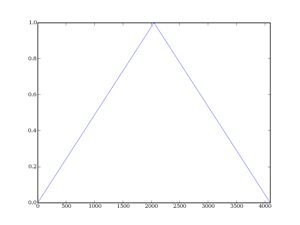
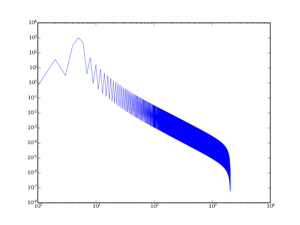
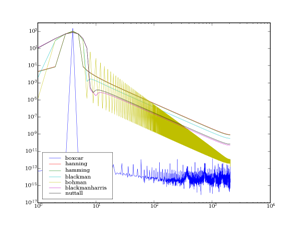
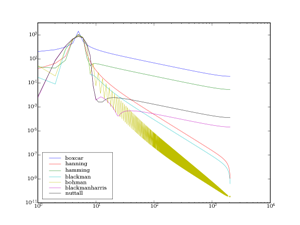
Chaque type de fenêtre a des spécificités sur les lobes secondaires et sur le lobe principal (largeur du lobe principal et amortissement des lobes secondaires principalement). Voici les deux signaux qui seront analysés :
Le lobe principal symbolise la fréquence fondamentale de la sinusoïde analysée (par exemple un sinus à 5 Hz possèdera un lobe principal centré autour des 5 Hz dans la représentation de Fourier) et les lobes secondaires représentent les « déchets » introduits par la distorsion due au fenêtrage (la sinusoïde tronquée n'est plus une sinusoïde du point de vue de la transformée de Fourier).
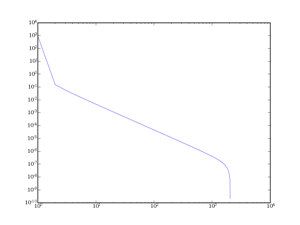
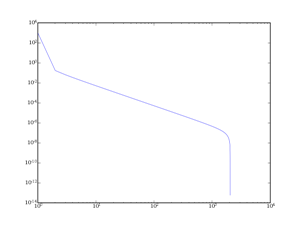
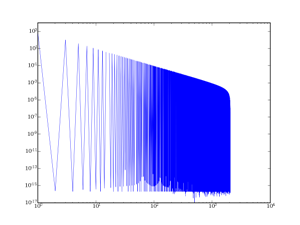
II-B-1. Le fenêtrage rectangulaire▲
La fenêtre rectangulaire est en fait simplement la fenêtre standard utilisée si on ne fait rien. En anglais, il s'agit de la fenêtre boxcar. On prend le signal et on regarde une partie, et la partie est sélectionnée par une fenêtre valant 0 ou 1. Le résultat est donc le suivant :
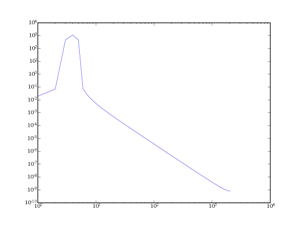
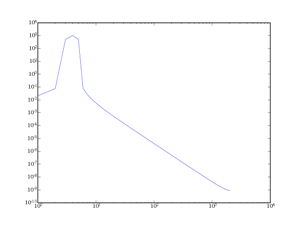
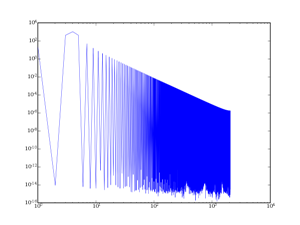
II-B-2. La fenêtre de Hamming▲
La fenêtre de Hamming est une fenêtre moyenne entre un lob principal étroit et un amortissement modéré des lobes secondaires. La formule de la fenêtre est la suivante :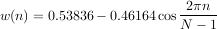 
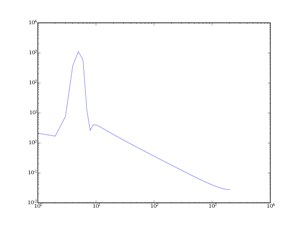
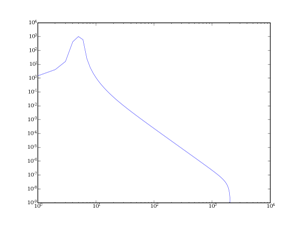
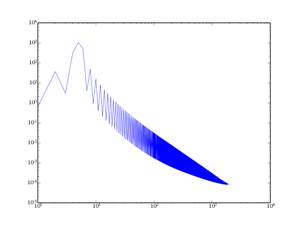
II-B-3. La fenêtre de Hann(ing)▲
La fenêtre de Hanning (ou plutôt Hann, du nom de son auteur) est elle aussi une fenêtre intermédiaire, comme Hamming. La formule de la fenêtre est la suivante :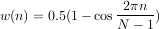 
II-B-4. Les fenêtres triangulaire et de Bartlett▲
Les fenêtres triangulaire et de Bartlett sont des fenêtres quasiment identiques. La seule différence consiste dans les valeurs minimales et maximales qui sont nulles pour la fenêtre de Bartlett et non nulles pour la fenêtre triangulaire. Cela entraîne une différence pour les valeurs en haute fréquence. La formule de la fenêtre triangulaire est la suivante :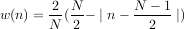 
. Celle de la fenêtre de Bartlett est :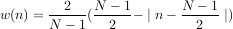 
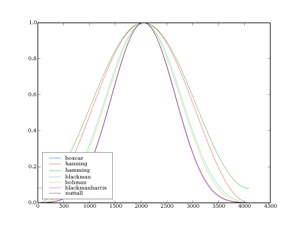
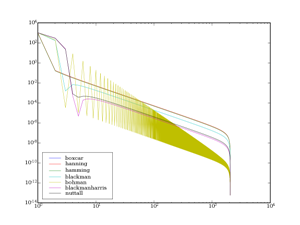
II-B-5. Résumé▲
De nombreuses autres fenêtres existent, certaines possèdent des paramètres de taille permettant de sélectionner la région la plus intéressante du signal (sachant que cela a une influence alors sur les lobes secondaires et la taille du lobe principal).
Si un sinus pur est parfaitement décrit par la FFT sans fenêtrage (ou alors avec fenêtrage rectangulaire), le cas d'un sinus tronqué montre clairement les avantages de ces fenêtres : certains ont un amortissement très rapide, mais au prix d'un lobe principal très large, donc avec une moins bonne précision sur la fréquence du sinus. Tout n'est que compromis.
III. La transformée de Fourier rapide (Cooley-Tukey)▲
Jusqu'à l'invention, ou plutôt la réinvention, de cet algorithme découvert initialement par Gauss, le calcul de la transformée de Fourier était en O(n²). L'amélioration de l'algorithme est permise grâce à la factorisation récursive de la formule générale.
L'algorithme original de Cooley-Tukey était dit radix-2. Cela signifie que la dimension était une puissance de 2, et la factorisation à l'échelle k fait appel à deux transformées de Fourier à l'échelle k-1. D'autres algorithmes par la suite ont d'autres radix pour des tailles qui ne sont pas des puissances de 2. Le meilleur site à ce sujet est celui de la FFTW.
Voici comment on arrive à la décomposition récursive :
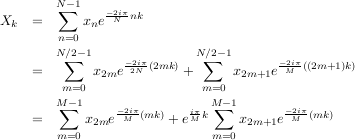
Une autre propriété est la suivante :
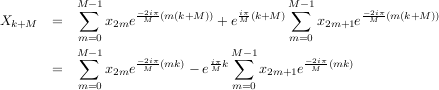
On effectue donc une FFT de taille inférieure sur les échantillons pairs et une autre sur les impairs à un facteur d'échelle près. La formule du radix-2 met en évidence une cellule de base qu'on appelle butterfly (on calcule simultanément deux coefficients de la FFT en prenant en compte la différence de signe des termes de la formule). On voit dans l'image suivante l'utilisation de ce butterfly pour résoudre ce problème.
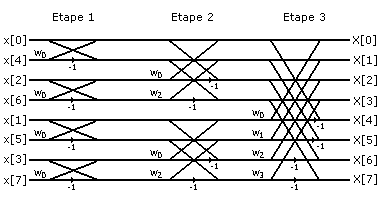
On peut réaliser la FFT entre deux espaces mémoire distincts ou en place, en écrasant le signal précédent. Dans ce cas, le résultat ne sera pas dans l'ordre et pour le retrouver, il faut permuter les bits des indices du tableau, comme indiqué dans le schéma précédent. Si un indice a la forme b3b2b1b0, l'indice dans la FFT correspondant est b0b1b2b3. C'est ce qu'on appelle le bit-reversal.
Pour la transformée inverse, on procède de la même manière avec l'exponentielle inverse. Dans les formules présentées, le facteur général de la FFT inverse n'est pas présenté. Il est possible de l'appliquer à la transformée directe, ou même en partie à la transformée directe et en partie à la transformée indirecte. Cela peut être judicieux – et indispensable en fait – dans le cas d'une FFT d'entiers.
IV. Conclusion▲
La présentation de la FFT ainsi que des outils indispensables pour l'utiliser, est maintenant finie, si vous désirez une utilisation, regardez le tuto de Florent sur FFTW ou dans le code utilisé pour générer les images pour Python.
Le code utilisé pour générer les images du fenêtrage est disponible ici.