I. Objectifs▲
Les objectifs de ce premier tutoriel sont simples :
- définir une architecture souple ;
- proposer une surcouche en Python pour simplifier les tests ;
- effectuer un ray tracing sans reflet ;
- optimiser le code.
Une bibliothèque matricielle doit être utilisée, une même classe servira pour chaque élément, vecteur point ou couleur, mais avec une taille différente si nécessaire. Pour bien séparer les responsabilités, un typedef sera utilisé pour chacun de ces éléments.
Pour le moment, les entrailles ne cette bibliothèque ne sont pas exposées, mais l'optimisation future de ce ray tracer passera par cette étape. Il est tout de même nécessaire d'utiliser une bibliothèque rapide.
Un vecteur aura pour type Vector3df, un point Point3df, une normale Normal3df et une couleur Color. Tous ces éléments et les autres classes vivront dans le namespace IRT.
II. Les classes de base▲
Les classes de base, outre les rayons qui seront exposés tout de suite, sont les chevilles ouvrières du ray tracer. Les primitives décrivent quels sont les objets qui peuvent être présents dans une scène, leur couleur à un endroit, s'ils sont transparents, s'ils reflètent la lumière (mat ou brillant)… La scène quant à elle agglomère ces primitives et permet de chercher de manière plus ou moins rapide ces éléments. Enfin, le ray tracer lui-même projette des rayons dans la scène et analyse les résultats.
Avant de commencer, la classe Ray va être exposée. Il s'agit en réalité d'une agrégation d'un vecteur et d'un point de départ.
class Ray
{
private:
Point3df origin_;
Vector3df direction_;
public:
_export_tools Ray(const Point3df& origin, const Vector3df& direction);
_export_tools ~Ray();
const Point3df& origin() const
{
return origin_;
}
Point3df& origin()
{
return origin_;
}
const Vector3df& direction() const
{
return direction_;
}
Vector3df& direction()
{
return direction_;
}
};Ma macro _export_tools permet d'exporter les symboles dans une bibliothèque dynamique sous Windows. Seuls les éléments accessibles de l'extérieur de la bibliothèque seront exportés.
Ray::Ray(const Point3df& origin, const Vector3df& direction)
:origin_(origin), direction_(direction)
{
}
Ray::~Ray()
{
}Cette classe ne nécessite pas plus de commentaires, tout le travail est réalisé par la bibliothèque matricielle.
II-A. Les primitives▲
Une primitive est tout objet qui pourra être contenu dans la scène, il s'agit donc d'une classe virtuelle pure, d'une interface, qui définit certaines fonctions virtuelles pures. Il s'agit du test de l'intersection ainsi que du calcul de la couleur :
class Primitive
{
public:
Primitive(){}
virtual ~Primitive()
{}
virtual bool intersect(const Ray& ray, float& dist) = 0;
virtual void computeColorNormal(const Ray& ray, float dist, Color& color, Vector3df& normal) = 0;
};Une primitive simple qui va être exposée est la classe Sphere qui permet d'instancier une sphère de couleur uniforme. Le calcul le plus complexe est celui de l'intersection entre un rayon et la sphère :
Sphere::Sphere(const Point3df& center, float radius)
:center(center), radius(radius), color(1.f)
{}
void Sphere::setColor(const Color& color)
{
this->color = color;
}
bool Sphere::intersect(const Ray& ray, float& dist)
{
float A = 1.f;
float B = (ray.direction() * (ray.origin() - center));
float C = norm2(ray.origin() - center) - radius * radius;
float delta = (B * B - À * C);
if(delta < 0.f)
return false;
float disc = sqrt(delta);
if(dist = - (B + disc) < 0.)
dist = - (B - disc);
return true;
}Le principe est de considérer le rayon comme une droite paramétrée par dist. À partir de cette équation, on rajoute l'équation de la sphère que le point doit respecter. Une équation du second degré doit alors être résolue et on prend la racine positive la plus petite en compte.
Pour simplifier les calculs, on considère que le vecteur direction du rayon est unitaire.
Il ne reste plus qu'à calculer la couleur si besoin est ainsi que la normale, ce qui est très simple pour une sphère connaissant son centre et le point sur la sphère que le rayon touche.
void Sphere::computeColorNormal(const Ray& ray, float dist, Color& color, Normal3df& normal)
{
Vector3df collide(ray.origin() + dist*ray.direction());
normal = collide - center;
normal *= 1./(sqrt(norm2(normal)));
color = this->color;
}La normale ne sera pas utilisée ici, tout comme la couleur est constante sur la scène.
II-B. La scène▲
Une scène regroupe donc les primitives. Il est nécessaire de pouvoir en ajouter, en ôter ou en récupérer une. De plus, c'est la scène qui est chargée de trouver un objet touché par un rayon à l'aide de la fonction getFirstCollision().
class SimpleScene
{
private:
std::vector<Primitive*> primitives;
public:
_export_tools SimpleScene();
_export_tools ~SimpleScene();
_export_tools Primitive* getPrimitive(unsigned long index);
_export_tools Primitive* removePrimitive(unsigned long index);
_export_tools long getFirstCollision(const Ray& ray, float& dist);
_export_tools bool addPrimitive(Primitive* primitive);
};Le code se charge de détruire les primitives qui sont stockées dans la scène. À partir du moment où une primitive est ajoutée dans la scène, celle-ci se charge de sa durée de vie. En revanche, si elle est ôtée de la scène, l'utilisateur doit la détruire lui-même.
Voici le code de la scène :
SimpleScene::SimpleScene()
:primitives()
{
}
SimpleScene::~SimpleScene()
{
for(std::vector<Primitive*>::const_iterator it = primitives.begin(); it != primitives.end(); ++it)
delete *it;
}
Primitive* SimpleScene::getPrimitive(unsigned long index)
{
return primitives[index];
}La primitive qui est ôtée de la scène est renvoyée à l'utilisateur :
Primitive* SimpleScene::removePrimitive(unsigned long index)
{
std::vector<Primitive*>::iterator it = primitives.begin();
std::advance(it, index);
Primitive* primitive = *it;
primitives.erase(it);
return primitive;
}Ceci est le cœur de la scène. Dans le cas simple présenté ici, chaque primitive est testée, et si le rayon touche la primitive, la distance du départ du rayon à la primitive est mise à jour dans dist et l'indice de la primitive est retourné.
long SimpleScene::getFirstCollision(const Ray& ray, float& dist)
{
float min_dist = std::numeric_limits<float>::max();
long min_primitive = -1;
for(std::vector<Primitive*>::const_iterator it = primitives.begin(); it != primitives.end(); ++it)
{
float dist;
bool test = (*it)->intersect(ray, dist);
if(test)
{
min_primitive = it - primitives.begin();
min_dist = dist;
}
}
if(min_primitive == -1)
return -1;
else
{
dist = min_dist;
return min_primitive;
}
}
bool SimpleScene::addPrimitive(Primitive* primitive)
{
if(std::find(primitives.begin(), primitives.end(), primitive) != primitives.end())
return false;
primitives.push_back(primitive);
return true;
}Une primitive ne peut être ajoutée deux fois dans la scène. Si l'insertion échoue, false est renvoyé par addPrimitive().
II-C. Le ray tracer▲
Un ray tracer peut utiliser a priori n'importe quelle scène à partir du moment où l'on peut obtenir la primitive touchée par un rayon.
class Raytracer
{
private:
void generateRay(unsigned long x, unsigned long y, Ray& ray) const;
void computeColor(const Ray& ray, Color& color) const;
void updateParameters();
public:
_export_tools Raytracer(unsigned long pixelWidth, unsigned long pixelHeight, float width, float height, float depth);
_export_tools ~Raytracer();
_export_tools void draw(float* screen) const;
_export_tools void setViewer(float width, float height, const Vector3df& origin, const Vector3df& direction);
_export_tools void setResolution(unsigned long pixelWidth, unsigned long pixelHeight);
_export_tools void setScene(SimpleScene* scene);
private:
Point3df origin;
Vector3df direction;
unsigned long pixelWidth;
unsigned long pixelHeight;
float width;
float height;
float depth;
float precompWidth;
float precompHeight;
SimpleScene* scene;
};Outre les fonctions clés du ray tracer, cette classe propose une interface permettant idéalement de positionner la caméra n'importe où (même si le code n'en est pas encore capable à l'heure actuelle).
Avant de commencer, quelques détails sur l'écran sont nécessaires. Il possède une hauteur et une largeur avec une certaine précision par dimension. L'écran se situe en plus à une certaine distance (profondeur) de l'observateur (la caméra). Ces éléments doivent être stockés dans la classe.
Raytracer::Raytracer(unsigned long pixelWidth, unsigned long pixelHeight, float width, float height, float depth)
:origin(0.), direction(0.), pixelWidth(pixelWidth), pixelHeight(pixelHeight), width(width), height(height), depth(depth)
{
direction(2) = 1;
updateParameters();
}
Raytracer::~Raytracer()
{
}Une fois ces éléments sauvegardés, une fonction de précalcul est appelée pour optimiser le temps d'exécution.
void Raytracer::generateRay(unsigned long x, unsigned long y, Ray& ray) const
{
ray.direction()(0) = precompWidth * (x - pixelWidth / 2.f);
ray.direction()(1) = precompHeight * (y - pixelHeight / 2.f);
ray.direction()(2) = depth;
ray.direction() *= 1./(sqrt(norm2(ray.direction())));
}Cette méthode construit un rayon unitaire sur place. À partir de la position de l'observateur, un rayon vers chaque pixel de l'écran est généré.
Générer le rayon sur place évite une copie de celui-ci à chaque étape : on gagne donc du temps.
Le code ici devrait tenir compte de la rotation de la caméra par rapport à la direction de l'écran.
void Raytracer::draw(float* screen) const
{
Ray ray(origin, direction);
for(unsigned long j = 0; j < pixelHeight; ++j)
{
for(unsigned long i = 0; i < pixelWidth; ++i)
{
generateRay(i, j, ray);
Color color(0.);
computeColor(ray, color);
for(unsigned int k = 0; k < nbColors; ++k)
screen[nbColors * (j* pixelWidth + i) + k] = color(k);
}
}
}Cette méthode permet de lancer le rayon dans une direction et de récupérer la couleur associée.
void Raytracer::setScene(SimpleScene* scene)
{
this->scene = scene;
}
void Raytracer::setResolution(unsigned long pixelWidth, unsigned long pixelHeight)
{
this->pixelWidth = pixelWidth;
this->pixelHeight = pixelHeight;
updateParameters();
}
void Raytracer::setViewer(float width, float height, const Vector3df& origin, const Vector3df& direction)
{
this->width = width;
this->height = height;
this->origin = origin;
this->direction = direction;
updateParameters();
}Ces différentes méthodes mettent à jour le ray tracer.
void Raytracer::computeColor(const Ray& ray, Color& color) const
{
float dist;
long index = scene->getFirstCollision(ray, dist);
if(index < 0)
return;
Normal3df normal;
Primitive* primitive = scene->getPrimitive(index);
primitive->computeColorNormal(ray, dist, color, normal);
}Le cœur du ray tracer teste s'il a touché une primitive et si c'est le cas récupère la couleur de l'objet. Par la suite, c'est lui aussi qui gèrera les rayons réfléchis et transmis.
void Raytracer::updateParameters()
{
precompWidth = width / pixelWidth;
precompHeight = height / pixelHeight;
}III. Encapsulation Python▲
Pour simplifier les tests et le développement, une partie du code est écrit en Python.
III-A. Création du wrapper▲
Le wrapper est un module SWIG qui s'appellera IRT. Pour gérer les vecteurs en Python, on utilisera Numpy.
Voici le cœur du module :
%{
#define SWIG_FILE_WITH_INIT
#define PY_ARRAY_UNIQUE_SYMBOL PyArray_API
%}
%include "numpy.i"
%init %{
import_array();
%}
%include "constraints.i"
%module(package="IRT", docstring="Python interface to the Interactive RayTracer") IRT
%nodefaultdtor;
%nodefaultctor;
%include "primitives.i"
%include "simple_scene.i"
%include "raytracer.i"Rien d'extraordinaire, à part qu'il n'existera pas d'encapsulation des constructeurs par défaut ou de recopie : cela évitera des bêtises.
III-A-1. Gestion des primitives▲
Cette partie est la plus complexe. En effet, il faut encapsuler chaque primitive, mais aussi gérer le fait que la scène gère la destruction d'une primitive si elle se trouve dans la scène.
La gestion des primitives par la scène est primordiale, en réalité. Si une primitive est ajoutée et que la scène ne gère pas sa destruction, la primitive sera détruite par Python à la sortie de la fonction de création de la scène, ce qui est gênant. Cela explique aussi la nécessité de gérer l'objet lorsqu'il est retiré de la scène.
%{
#include "primitives.h"
%}
%typemap(in)
(IRT::Vector3df&)
(PyArrayObject* array=NULL, int is_new_object=0)
{
array = obj_to_array_contiguous_allow_conversion($input, NPY_FLOAT, &is_new_object);
if (!array || !require_dimensions(array, 1) || (array->dimensions[0] != 3)) SWIG_fail;
$1 = new IRT::Vector3df((float*) array->data);
}
%typemap(freearg)
(IRT::Vector3df&)
{
if (is_new_object$argnum && array$argnum) Py_DECREF(array$argnum);
}
%typemap(in)
(IRT::Color& color)
(PyArrayObject* array=NULL, int is_new_object=0)
{
array = obj_to_array_contiguous_allow_conversion($input, NPY_FLOAT, &is_new_object);
if (!array || !require_dimensions(array, 1) || (array->dimensions[0] != IRT::nbColors)) SWIG_fail;
$1 = new IRT::Color((float*) array->data);
}
%typemap(freearg)
(IRT::Color&)
{
if (is_new_object$argnum && array$argnum) Py_DECREF(array$argnum);
}On voit l'apparition de IRT::nbColors. Cette constante indique en réalité le nombre de couleurs gérées par le ray tracer.
Lorsqu'un tableau Numpy est passé en paramètre à une fonction prenant un vecteur en paramètre, une référence sur cet objet est acquise et n'est libérée qu'à la fin de la fonction par le typemap freearg.
%typemap(in) IRT::Primitive*
{
if ((SWIG_ConvertPtr($input,(void **)(&$1),$1_descriptor, SWIG_POINTER_EXCEPTION | SWIG_POINTER_DISOWN)) == -1) SWIG_fail;
}
%typemap(out) IRT::Primitive*
{
$result = SWIG_NewPointerObj($1, $1_descriptor, SWIG_POINTER_OWN);
}Ces typemaps sont chargés de déléguer la gestion de l'objet ou de récupérer la gestion lors de l'interaction avec la scène.
namespace IRT
{
class Primitive
{
public:
~Primitive();
};
class Sphere: public Primitive
{
public:
Sphere(IRT::Vector3df& ray, float dist);
~Sphere();
void setColor(IRT::Color& color);
};
}Il est à noter que toute l'interface n'est pas accessible en Python. Cela est normal, il n'est pas nécessaire et peu judicieux de laisser l'accès aux entrailles du ray tracer à tout un chacun.
III-A-2. Gestion de la scène▲
La scène doit permettre d'ajouter ou de retirer un élément. Seuls ces éléments sont pertinents.
%{
#include "simple_scene.h"
%}
%apply Pointer NONNULL{IRT::Primitive*};
namespace IRT
{
class SimpleScene
{
public:
SimpleScene();
~SimpleScene();
IRT::Primitive* removePrimitive(unsigned long index);
bool addPrimitive(IRT::Primitive* primitive);
};
}Si un pointeur NULL est passé à la fonction, le wrapper SWIG lèvera lui-même une exception. Cette contrainte est contenue dans le fichier constraints.i ajouté dans IRT.i.
III-A-3. Gestion du ray tracer▲
%{
#include "raytracer.h"
%}
%typecheck(SWIG_TYPECHECK_DOUBLE_ARRAY)
(float* INPLACE_ARRAY)
{
$1 = is_array($input) && PyArray_EquivTypenums(array_type($input),NPY_FLOAT);
}
%typemap(in)
(float* INPLACE_ARRAY)
(PyArrayObject* array=NULL, int is_new_object=0)
{
array = obj_to_array_contiguous_allow_conversion($input, NPY_FLOAT, &is_new_object);
$1 = ($1_ltype) array->data;
}
namespace IRT
{
class Raytracer
{
public:
Raytracer(unsigned long pixelWidth, unsigned long pixelHeight, float width, float height, float depth);
~Raytracer();
void draw(float* INPLACE_ARRAY);
void setResolution(unsigned long pixelWidth, unsigned long pixelHeight);
void setScene(IRT::SimpleScene* scene);
};
}Le ray tracer doit pouvoir récupérer une scène, dessiner celle-ci et décider de sa résolution. Le point le plus critique reste le dessin de la scène, ici implémenté grâce à un typemap in qui donne accès au tableau Numpy sous-jacent.
III-B. Création d'une scène et mesure de temps▲
Pour tester la vitesse d'exécution et en effectuer un profil, il est nécessaire de tout d'abord créer la scène et le raytracer puis dans une autre fonction ou méthode appeler la méthode draw() du raytracer.
import IRT
import numpy
class Sample(object):
def __init__(self):
self.raytracer = IRT.Raytracer(800, 600, 8., 6., 40.)
self.scene = IRT.SimpleScene()
sphere = IRT.Sphere(numpy.array((0, 0, 80.), dtype=numpy.float32), 2.)
sphere.setColor(numpy.array((0., 0., 1.), dtype=numpy.float32))
self.scene.addPrimitive(sphere)
sphere = IRT.Sphere(numpy.array((2., 1., 60.), dtype=numpy.float32), 1.)
sphere.setColor(numpy.array((1., 0., 0.), dtype=numpy.float32))
self.scene.addPrimitive(sphere)
sphere = IRT.Sphere(numpy.array((-2., -1., 60.), dtype=numpy.float32), 1.)
sphere.setColor(numpy.array((0., 1., 0.), dtype=numpy.float32))
self.scene.addPrimitive(sphere)
self.raytracer.setScene(self.scene)
def __call__(self, screen):
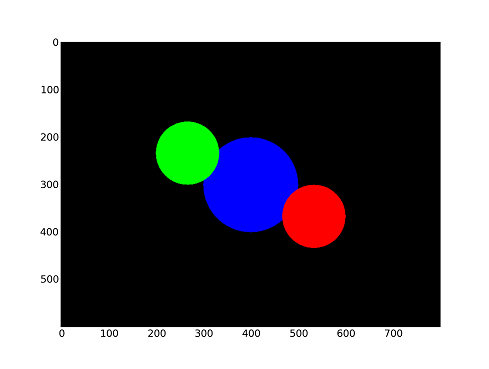
self.raytracer.draw(screen)L'écran est de taille 800x600, avec une résolution de 0.1 par pixel. Trois sphères seront dessinées devant l'écran, une en bleu, une en vert et une dernière en rouge. La méthode __call__() sera utilisée pour mesurer le temps d'exécution ou créer le profil.
import timeit
setup="""import numpy
import sample
import pylab
s = sample.Sample()
screen = numpy.zeros((600, 800, 3), dtype=numpy.float32)
"""
timer = timeit.Timer('s(screen)', setup=setup)
print timer.timeit(10)IV. Résultats▲
IV-A. Résultat brut▲
IV-B. Profil du raytracer▲
Avant de parler profil, le ray tracer trace cette simple scène en 140 ms sur un Xeon 3.8GHz sous Linux avec GCC 4.1.2. Sous Windows, avec un Athlon 64 3000+ (1.8GHz),il faut près d'une demi-seconde pour dessiner cette scène. Malheureusement, les outils de profil sont plus rares sous Windows, il est donc plus complexe de déterminer un profil pour déterminer le point critique.
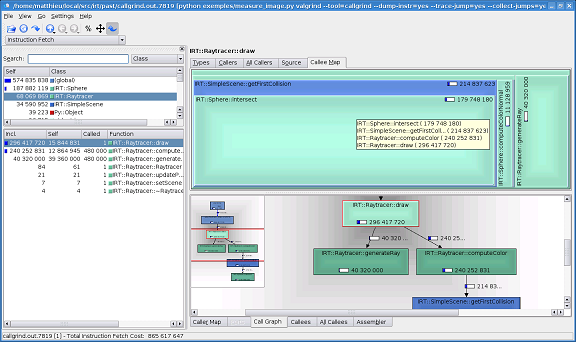
Voici donc ce profil en mode optimisé calculé par Valgrind, sous Linux :
La majorité du temps est passé dans la fonction de calcul d'intersection, et plus particulièrement dans les fonctions de la bibliothèque matricielle d'addition ou de soustraction. Cela peut se voir en observant les coûts par instruction, grâce à KCacheGrind. Ces trois éléments sont pour le moment le principal frein de notre fonction. En particulier, aucune instruction SSE n'est générée par aucun des compilateurs testés (MSVC, GCC ou Intel).
V. Conclusion▲
Je vous ai présenté une base de travail pour un ray tracer interactif. Les prochains tutoriels proposeront :
- la gestion des reflets et des lumières ;
- le suréchantillonnage ;
- …