Introduction▲
Les graphes proposés par Boost sont très particuliers. En eux-mêmes, ils ne font rien. En revanche, Boost.Graph (BGL pour les intimes - propose un nombre important de fonctions libres qui permettent d'utiliser les algorithmes avec n'importe quelle structure de données. Cela a une importance que l'on verra par la suite. En ce qui concerne les propriétés des arcs ou des sommets, Boost.Graph utilise les Property Maps disponibles dans Boost.
I. Concepts de graphes▲
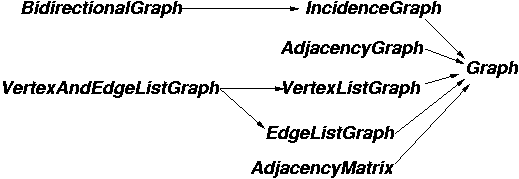
Avant de parler implémentation, parlons de concepts sur les graphes, tels que Boost.Graph les voit.
I-A. Graph▲
Le concept de base est le celui de Graph. Il requiert la définition de plusieurs types de données, exposés dans le tableau suivant, avec G le type de graphe utilisé.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: vertex_descriptor |
Type des sommets |
|
boost::graph_traits<G>:: edge_descriptor |
Type des arcs |
|
boost::graph_traits<G>:: directed_category |
Directivité des arcs, valant directed_tag ou undirected_tag |
|
boost::graph_traits<G>:: edge_parallel_category |
Indique si plusieurs arcs pour le mĂŞme couple (u, v) peuvent coexister, valant allow_parallel_edge_tag ou disallow_parallel_edge_tag |
|
boost::graph_traits<G>:: traversal_category |
Donne le type de visites dans les arcs et les sommets, prenant les valeurs incidence_graph_tag, adjacency_graph_tag, bidirectional_graph_tag, vertex_list_graph_tag, edge_list_graph_tag ou adjacency_matrix_tag |
Avec ces cinq expressions, on a la correspondance avec la théorie des graphes en entier. Multigraphes, graphes simples, tout est possible facilement. Naturellement, selon les valeurs de ces tags, certains algorithmes auront du mal à fonctionner, et c'est ce que nous verrons dans les prochains tutoriels.
Pour rentrer un peu plus dans les détails, un Graph n'est pas forcément copiable, contrairement aux boost::graph_traits<G>::vertex_descriptor et aux boost::graph_traits<G>::edge_descriptor qui doivent être copiables, avoir un constructeur par défaut valide et avoir un opérateur d'égalité valide.
Pour finir, on doit disposer d'une fonction.
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
boost::graph_traits<G>:: null_vertex() |
boost::graph_traits<G>:: vertex_descriptor |
Retourne un vertex nul sans rapport avec un graphe de type G |
I-B. IncidenceGraph▲
Ce type de graphe est une spécialisation du concept de Graph. Il permet un accès efficace aux arcs partant d'un sommet.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: traversal_category |
Doit pouvoir se convertir en incidence_graph_tag |
|
boost::graph_traits<G>:: out_edge_iterator |
Permet d'itérer sur les arcs d'un graphe partant d'un sommet |
|
boost::graph_traits<G>:: degree_size_type |
Type entier représentant le nombre d'arcs partant d'un sommet |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
source(e, g) |
boost::graph_traits<G>:: vertex_descriptor |
Retourne le sommet source d'un arc e dans un graphe g |
|
target(e, g) |
boost::graph_traits<G>:: vertex_descriptor |
Retourne le sommet cible d'un arc e dans un graphe g |
|
out_edges(u, g) |
std::pair <boost::graph_traits<G>:: out_edge_iterator, boost::graph_traits<G>:: out_edge_iterator> |
Retourne une paire d'itérateurs sur des arcs sortants du sommet u dans le graphe g |
|
out_edges(u, g) |
boost::graph_traits<G>:: degree_size_type |
Retourne le nombre d'arcs partants de u dans le graphe g |
Les fonctions source(), target(), and out_edges() doivent être en temps constant, quant à out_degree(), elle doit être en temps linéaire du nombre d'arcs sortants.
On voit dans ces exemples de fonctions qui doivent être valides que l'implémentation avec des fonctions libres permet d'utiliser librement celles-ci avec n'importe quel IndidenceGraph.
I-C. BidirectionalGraph▲
Ce raffinement de IncidenceGraph prend en charge l'itération sur les arcs aboutissant à une cible. La différenciation du type parent est due à la place mémoire plus importante occupée par de tels graphes et parce que tous les arguments n'ont pas besoin d'accéder à la liste des arcs aboutissant à un sommet.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: traversal_category |
Doit pouvoir se convertir en bidirectional_graph_tag |
|
boost::graph_traits<G>:: in_edge_iterator |
Permet d'itérer sur les arcs d'un graphe incident à un sommet |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
in_edges(u, g) |
std::pair <boost::graph_traits<G>:: in_edge_iterator, boost::graph_traits<G>:: in_edge_iterator> |
Retourne une paire d'itérateurs sur des arcs partant d'un sommet u dans le graphe g |
|
in_degree(v, g) |
boost::graph_traits<G>:: degree_size_type |
Retourne le nombre d'arcs incidents Ă v dans le graphe g |
|
degree(v, g) |
boost::graph_traits<G>:: degree_size_type |
Retourne le nombre d'arcs incidents Ă v et partant de v dans le graphe g |
La fonction in_edges() est en temps constant, tandis que les autres fonctions ont un temps linéaire en relation avec le nombre d'arcs aboutissant.
I-D. AdjacencyGraph▲
Ce raffinement de Graph permet d'itérer sur les sommets adjacents à un autre sommet, contrairement au concept IncidenceGraph qui permet une itération sur les arcs adjacents à un sommet.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: traversal_category |
Doit pouvoir se convertir en adjacency_graph_tag |
|
boost::graph_traits<G>:: adjacency_iterator |
Permet d'itérer sur les sommets adjacents à un autre sommet dans un graphe |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
adjacent_vertices(u, g) |
std::pair <boost::graph_traits<G>:: adjacency_iterator, boost::graph_traits<G>:: adjacency_iterator> |
Retourne une paire d'itérateurs sur des sommets adjacents à un sommet u dans le graphe g |
La fonction adjacent_vertices() est exécutée en temps constant.
I-E. VertexListGraph▲
VertexListGraph est un concept un peu particulier puisqu'il ne travaille que sur les sommets, contrairement aux précédents qui avaient une notion d'arc.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: traversal_category |
Doit pouvoir se convertir en vertex_list_graph_tag |
|
boost::graph_traits<G>:: vertex_iterator |
Permet d'itérer sur les sommets d'un graphe |
|
boost::graph_traits<G>:: vertices_size_type |
Type entier qui peut contenir le nombre de sommets d'un graphe |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
vertices(g) |
std::pair <boost::graph_traits<G>:: vertex_iterator, boost::graph_traits<G>:: vertex_iterator> |
Retourne une paire d'itérateurs sur les sommets du graphe g |
|
num_vertices(g) |
boost::graph_traits<G>:: vertices_size_type |
Retourne le nombre de sommets du graphe g |
vertices() doit s'exécuter en temps constant.
I-F. EdgeListGraph▲
EdgeListGraph est un concept parallèle au précédent puisqu'il ne travaille que sur les arcs.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: traversal_category |
Doit pouvoir se convertir en edge_list_graph_tag |
|
boost::graph_traits<G>:: edge_iterator |
Permet d'itérer sur les arcs d'un graphe |
|
boost::graph_traits<G>:: edges_size_type |
Type entier qui peut contenir le nombre d'arcs d'un graphe |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
edges(g) |
std::pair <boost::graph_traits<G>:: edge_iterator, boost::graph_traits<G>:: edge_iterator> |
Retourne une paire d'itérateurs sur les arcs du graphe g |
|
num_edges(g) |
boost::graph_traits<G>:: edges_size_type |
Retourne le nombre d'arcs du graphe g |
|
source(e, g) |
boost::graph_traits<G>:: vertex_descriptor |
Retourne le sommet source d'un arc e dans un graphe g |
|
boost::graph_traits<G>:: target(e, g) |
boost::graph_traits<G>:: vertex_descriptor |
Retourne le sommet cible d'un arc e dans un graphe g |
Les fonctions edges(), source() et target() doivent s'exécuter en temps constant.
I-G. VertexAndEdgeListGraph▲
VertexAndEdgeListGraph est un concept regroupant les deux précédents, à savoir VertexListGraph et EdgeListGraph, sans autres définitions supplémentaires.
I-H. AdjacencyMatrix▲
AdjacencyMatrix est un concept permettant d'accéder directement à n'importe arc connaissant sa source et sa cible.
|
Type |
Explication |
|---|---|
|
boost::graph_traits<G>:: traversal_category |
Doit pouvoir se convertir en adjacency_matrix_tag |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
edge(u,v,g) |
std::pair <boost::graph_traits<G>:: edge_descriptor, bool> |
Retourne un drapeau indiquant s'il existe un arc entre u et v, ainsi que l'arc en question si la réponse est positive |
Les fonctions edges(), source() et target() doivent s'exécuter en temps constant.
I-I. MutableGraph▲
MutableGraph ne se trouve pas sur le schéma, mais consiste à permettre la modification d'un graphe.
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
add_edge(u, v, g) |
std::pair <boost::graph_traits<G>:: edge_descriptor, bool> |
Crée un nouvel arc s'il n'existe pas ou si le graphe peut avoir des arcs parallèles et retourne un drapeau placé à true, ajoute un arc entre u et v, ainsi que l'arc en question |
|
remove_edge(u, v, g) |
void |
Efface tous les arcs entre u et v, attention, une précondition est qu'il existe un tel arc |
|
remove_edge(e, g) |
void |
Efface l'arc e dans le graphe g |
|
remove_edge(iter, g) |
void |
Efface l'arc pointé par l'itérateur d'arc iter dans le graphe g, valable si le graphe est un modèle de IncidenceGraph |
|
remove_edge_if(p, g) |
void |
Efface tous les arcs du graphe g pour lequel le prédicat p est vrai. |
|
remove_out_edge_if(u, p, g) |
void |
Efface les arcs incidents à u dans le graphe g si le prédicat p est vrai, valable si le graphe est un modèle de IncidenceGraph |
|
remove_in_edge_if(v, p, g) |
void |
Efface les arcs partant de v dans le graphe g si le prédicat p est vrai, valable si le graphe est un modèle de BidirectionalGraph |
|
add_vertex(g) |
boost::graph_traits<G>:: vertex_descriptor |
Crée un nouveau sommet dans le graphe g et renvoie son descripteur |
|
boost::graph_traits<G>:: clear_vertex(u, g) |
void |
Efface tous les arcs incidents et partants de u dans le graphe g |
|
boost::graph_traits<G>:: remove_vertex(u, g) |
void |
Efface le sommet u du graphe g, sachant qu'il n'y a plus d'arc incident ou partant de ce sommet |
II. Les propriĂ©tĂ©s des arcs▲
Tous ces concepts sont bien beaux, mais il faut pouvoir attacher aux sommets ou aux arcs des valeurs autres que leurs descripteurs pour certains algorithmes, comme le coût, un débit maximal… Pour cela, deux autres concepts de graphes sont à utiliser.
II-A. PropertyGraph▲
Ce graphe permet d'associer aux sommets ou aux arcs des propriétés. Afin de les distinguer, on utilise des tags, et selon le tag donné, une fonction permet de récupérer la PropertyMap associée.
|
Type |
Explication |
|---|---|
|
boost::property_map<G, PropertyTag>:: type |
Le type de la PropertyMap pour le tag PropertyTag associé doit être un modèle de ReadWritePropertyMap |
|
boost::property_map<G, PropertyTag>:: const_type |
Le type de la PropertyMap pour le tag PropertyTag associé doit être un modèle de ReadablePropertyMap |
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
get(p, g) |
boost::property_map <G, PropertyTag>::type ou boost::property_map <G, PropertyTag>::const_type si G n'est pas mutable |
Retourne la PropertyMap associée au tag p dans le graphe g |
|
get(p, g, x) |
boost::property_traits<Map>:: value_type |
Retourne la propriété de la PropertyMap associée au tag p dans le graphe g pour le sommet ou l'arc x |
|
put(p, g, x, v) |
void |
Enregistre la valeur v dans la propriété indiquée par le tag p du sommet ou arc x du graphe g |
La fonction get() s'exécute en temps constant.
II-B. MutablePropertyGraph▲
Ce concept permet d'ajouter un arc ou un sommet avec certaines propriétés.
|
Nom |
Type de retour |
Explication |
|---|---|---|
|
add_edge(u, v, ep, g) |
std::pair<edge_descriptor, bool> |
Insère l'arc (u, v) dans le graphe g avec la propriété ep |
|
add_vertex(vp, g) |
vertex_descriptor |
Crée un nouveau sommet dans le graphe g avec la propriété vp |
II-C. Gestion des propriĂ©tĂ©s dans les algorithmes de graphes▲
On peut utiliser des propriétés internes ou externes dans un algorithme de graphes. Par exemple, l'algorithme de Djikstra utilise quatre propriétés différentes. Au lieu de spécifier à chaque fois ces propriétés lors de l'appel, on peut utiliser les propriétés internes, assouplissant donc les appels aux algorithmes.
II-C-1. Les propriĂ©tĂ©s internes▲
Ces propriétés ont la même durée de vie que le graphe lui-même. Par exemple, si on stocke des poids sur un arc dans le graphe, pour les récupérer, on exécutera l'instruction suivante :
property_map<Graph, vertex_distance_t>::type d = get(vertex_distance, g);La propriété vertex_distance_t est intérieure, car pour l'obtenir, on fait une requête sur le graphe g. Remarquez que le type est vertex_distance_t quand le tag utilisé pour récupérer cette propriété est vertex_distance. Les algorithmes de parcours ont besoin de ces propriétés pour fonctionner. Par exemple, l'algorithme de Dijkstra nécessite quatre propriétés et serait appelé ainsi pour un graphe g et un sommet source src :
dijkstra_shortest_paths(g, src,
distance_map(get(vertex_distance, g)).
weight_map(get(edge_weight, g)).
color_map(get(vertex_color, g)).
vertex_index_map(get(vertex_index, g)));Grâce aux propriétés intérieures, on peut utiliser des propriétés par défaut, et n'appeler la méthode qu'avec deux paramètres :
dijkstra_shortest_paths(g, src);II-C-2. Les propriĂ©tĂ©s externes▲
Il existe plusieurs méthodes pour créer des propriétés extérieures.
La première méthode utilise la classe random_access_iterator_property_map. À partir d'un identifiant unique récupéré d'une propriété du graphe – par exemple edge_index qui renvoie… un index –. On peut trouver un exemple ici.
La deuxième solution utilise un pointeur comme type. On doit alors utiliser un entier comme index de parcours, ce qui est le cas si le graphe qu'on utilise est un adjacency_list avec VertexList=vecS. Pour savoir ce que cela veut dire, reportez-vous au prochain chapitre ;). Un exemple utilisant cette technique se trouve aussi sur le site de Boost ici.
III. Les classes proposĂ©es▲
III-A. adjacency_list▲
De son nom complet adjacency_list<OutEdgeList, VertexList, Directed, VertexProperties, EdgeProperties, GraphProperties, EdgeList>, ce qui indique la complexité et la versatilité de cette classe. Cette classe implémente, comme son nom l'indique, un graphe sous la forme de liste d'adjacence. Mais ce n'est pas tout, car il est possible de spécifier si la liste des sommets est une liste ou un vecteur ou autre, de même pour la liste des arcs. On verra dans une prochaine sous-partie les valeurs possibles et leurs implications.
Les termes suivants indiquent si le graphe est orienté – la valeur par défaut est directedS, mais elle peut valoir undirectedS ou bidirectionalS –, les termes templates suivants indiquent les propriétés internes du graphe, le dernier terme propose un stockage de la liste de tous les arcs du graphe.
III-A-1. Les possibilitĂ©s pour OutEdgeList, VertexList et EdgeList▲
On peut utiliser chaque conteneur de la STL pour le stockage. La liste des types équivalents à ces conteneurs est donnée ici :
- vecS correspond à std::vector ;
- listS correspond à std::list ;
- slistS correspond à std::slist ;
- setS correspond à std::set ;
- multisetS correspond à std::multiset ;
- hash_setS correspond Ă std::hash_set.
Chaque sélection de conteneur a ses inconvénients pour ce qui est de l'insertion, de la recherche ou de l'effacement. Choisissez judicieusement l'un ou l'autre selon vos besoins.
Une dernière attention doit être portée à la destruction de sommets dans le graphe. Il n'existe qu'une seule fonction, vertices(), qui retourne deux itérateurs sur le début et la fin de la liste des sommets. Seulement, lorsqu'on choisit vecS comme liste des sommets, la destruction d'un des sommets entraîne l'invalidation des itérateurs…
III-A-2. Les propriĂ©tĂ©s internes des sommets et arcs▲
Ici encore, deux solutions sont proposées.
La première utilise la récursivité sur les Property Maps grâce au dernier paramètre template. Un exemple rapide :
boost::property<boost::vertex_name_t, std::string,
boost::property<population_t, int,
boost::property<zipcodes_t, std::vector<int> > > >Trois propriétés sont définies, la première est le nom du sommet, avec une chaîne de caractères, la deuxième contient une population à l'aide d'un entier, la dernière étant un code postal enregistré dans un vecteur d'entiers.
L'autre solution, les bundle properties, consiste simplement à déclarer une structure de données contenant les champs que l'on veut :
struct Ville
{ std::string nom;
int population;
std::vector<int> codePostal;
}On utilise alors directement le nom de la structure dans le paramètre template du graphe. Mais maintenant, comment utiliser ces valeurs comme propriétés internes ? En fait, ce n'est pas possible, pour cette solution, il faut utiliser la méthode précédente. Pour récupérer la Property Map associée au nom, il faut faire un :
get(&Ville::nom, g)Pour créer une carte de distance entre les villes, si on possède une structure Route :
weight_map(get(&Route::kilometres, g))
.distance_map(make_iterator_property_map(distances.begin(),
get(vertex_index, g)))Un peu compliqué par rapport à la méthode précédente, surtout que c'est ce qu'il faut indiquer aux algorithmes lors de la sélection des propriétés sur lesquelles faire les calculs ! Autant dire que la première méthode, même si elle n'est plus recommandée, est sacrément plus utilisable.
III-B. adjacency_matrix▲
La représentation sous forme de matrice d'adjacence a moins de propriétés, logiquement. Directed, VertexProperty, EdgeProperty, GraphProperty, Allocator sont modifiables, quoique la dernière valeur n'est que rarement spécifiée - autant garder la valeur par défaut -. Pour les autres valeurs, elles sont identiques à l'adjacency_list, sauf pour Directed qui ne prend que les valeurs directedS ou undirectedS.
III-C. Les classes de conversion ou d'adaptation▲
Plusieurs classes sont proposées pour les adapter aux exigences de Boost.
III-C-1. subgraph▲
La création de sous-graphes permet de travailler sur certaines parties d'un graphe. Lors de la création d'un nouveau graphe, il suffit de créer les sous-graphes, d'attacher les sommets et les arcs adéquats aux sous-graphes et au graphe.
III-C-2. edge_list▲
Le type complet est edge_list<EdgeIterator, ValueType, DiffType> et permet d'adapter une série d'itérateurs sur des arcs en une liste d'arc, modélisant par la même occasion EdgeListGraph. Le premier paramètre template correspond au type d'itérateur utilisé, les deux suivants correspondent par défaut à std::iterator_traits<EdgeIterator>::value_type et std::iterator_traits<EdgeIterator>::difference_type.
III-C-3. reverse_graph▲
À partir d'un graphe bidirectionnel, on peut créer un graphe dont le sens des arcs est inversé.
III-C-4. filtered_graph▲
Le dernier adaptateur dont il sera question est l'adaptateur qui permet de filtrer les sommets et arcs d'un autre graphe. Il possède trois paramètres template, le premier correspondant au type de graphe, le deuxième au prédicat pour les sommets et le troisième concerne le prédicat pour les arcs.
III-C-5. D'autres adaptateurs▲
Il existe d'autres adaptateurs permettant de voir un vecteur ou une matrice comme un pointeur vers un graphe, ou alors permettant d'encapsuler des types de graphes existant comme le graphe Leda ou le Stanford GraphBase.
IV. Rapide exemple▲
On va voir un petit exemple pour remplir un graphe et l'afficher.
Pour réaliser le test, on va utiliser une structure de liste d'adjacence - adjacency_list - avec un vecteur pour stocker les sommets et une liste pour les arcs. À partir d'une matrice de distance entre les points, on va retourner un graphe des plus proches voisins.
#include <iostream>
#include <boost/graph/adjacency_list.hpp>
/// Defaut type of a graph
typedef boost::adjacency_list<boost::listS, boost::vecS, boost::directedS,
boost::property<boost::vertex_index_t, unsigned int>,
boost::property<boost::edge_weight_t, double > > Graph;
/// Vertex map type
typedef boost::property_map<Graph, boost::vertex_index_t>::type VertexIndexMapT;
/// Defaut type of a vertex in a graph
typedef boost::graph_traits<Graph>::vertex_descriptor Vertex;
/// Edge map type
typedef boost::property_map<Graph, boost::edge_weight_t>::type EdgeIndexMapT;
/// Defaut type of an edge in a graph
typedef boost::graph_traits<Graph>::edge_descriptor Edge;
/// Edge iterator
typedef boost::graph_traits<Graph>::edge_iterator EdgeIterator;
/// Creates graphs from matrix with K-neighbooring
struct FromMatrixKNeighboor
{
/**
* Constructor of a Parzen factory
* @param neighboor is the number of neighboors to consider
*/
FromMatrixKNeighboor(const unsigned int neighboor)
:neighboor(neighboor)
{
}
/**
* Creates a graph from an points matrix
* @param pointsMatrix is the points matrix
* @return a graph with the vertices being the point in pointsMatrix
* and the egdes between some points have a max distance
* @sa distance
*/
template<class Matrix>
const Graph create(const Matrix& pointsMatrix) const
{
Graph g;
VertexIndexMapT index = get(boost::vertex_index, g);
EdgeIndexMapT distances = get(boost::edge_weight, g);
unsigned int nbPoints = pointsMatrix.width();
for(unsigned int i = 0; i < nbPoints; ++i)
{
add_vertex(g);
}
std::vector<std::multimap<DataType, unsigned int> > calculatedDistances(nbPoints);
for(unsigned int i = 0; i < nbPoints; ++i)
{
for(unsigned int j = i + 1; j < nbPoints; ++j)
{
DataType dist(matrix::norm2(pointsMatrix[i] - pointsMatrix[j]));
calculatedDistances[i].insert(std::pair<DataType, unsigned int>(dist, j));
calculatedDistances[j].insert(std::pair<DataType, unsigned int>(dist, i));
}
}
for(unsigned int points = 0; points < nbPoints; ++points)
{
unsigned int neighboorNumber = 0;
for(typename std::multimap<DataType, unsigned int>::iterator potentialEdge
= calculatedDistances[points].begin();
(potentialEdge != calculatedDistances[points].end()) && (neighboorNumber < neighboor);
++potentialEdge, ++neighboorNumber)
{
Edge newEdge;
bool inserted;
boost::tie(newEdge, inserted)= add_edge(points, potentialEdge->second, g);
distances[newEdge] = DataTypeTraits<DataType>::sqrt(potentialEdge->first);
}
}
EdgeIterator first, last;
for(boost::tie(first, last) = edges(g); first != last; ++first)
{
std::cout << boost::source(*first, g) << " to " << boost::target(*first, g) << " = ";
std::cout << boost::get(distances, *first) << std::endl;
}
return g;
}
private:
/// Storage of the size of the neighboorhood
unsigned int neighboor;
};On utilise une classe pour gérer cette construction du graphe des plus proches voisins. Une fonction particulière, boost::tie, est utilisée pour assigner automatiquement une paire de variables à une paire de variables, elle permet de gagner du temps d'écriture.
En regardant ce code, on voit trois parties, la première créée les sommets, la seconde les arcs potentiels partant d'un point tandis que la troisième sélectionne les meilleurs éléments.
Puisque notre graphe utilise un vecteur pour stocker les sommets, il y a équivalence entre un entier non signé et le type Vertex, ce qui simplifie le code. On voit aussi l'utilisation ici d'une property map interne, edge_weight, qui contiendra les distances entre les sommets dans le graphe.
Conclusion▲
L'implémentation de la BGL correspond à ce qu'on peut attendre d'un graphe. Les fonctions proposées servent de fondations pour les autres fonctions que nous étudierons par la suite.
Un gros avantage de la bibliothèque provient aussi de sa volonté de versatilité, car outre les deux types de base utilisables par tous les algorithmes, il y a aussi les adaptateurs qui permettent d'éviter des conversions inutiles.





